旧来、林業は、木材を提供するという産業でしたが、最近では、環境的な役割や、エコツーリズムなど別の産業と結びつける役割も担うようになりました。森林の中で、伐採する場所や野生動物を保護する地区を設定することは、「森林のランドスケープ管理」と呼ばれ、景観のみならず、生物多様性の保全や野生動物の生息地の形成に不可欠となっています。

環境問題を統計数理モデルで解く

統計数理研究所の吉本敦教授は、さまざまな現象を数式で表す「統計数理モデル」を活用し、森林資源の最適な管理を考えています。「環境保全と経済発展など競合する利用が生じた場合、その資源をどのように配分したらいいのかと考えることが必要で、これは最適化問題として解決できます」（同教授）（図）。

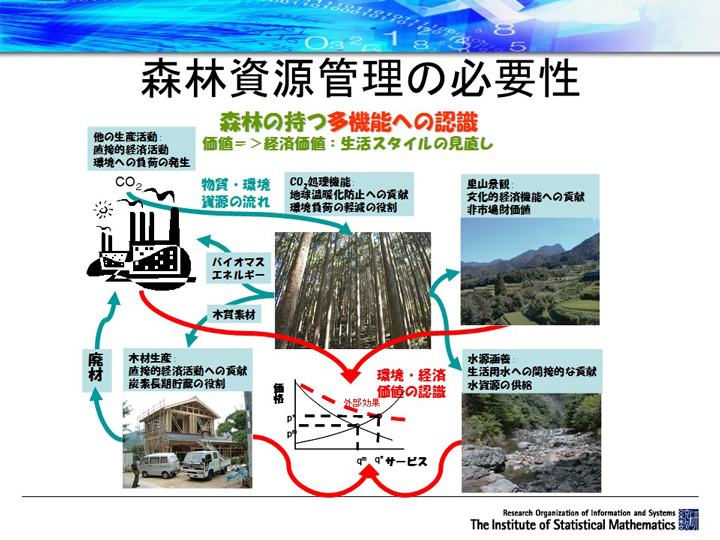
森林の中で、ある特定の場所に同種・同齢の木が集まっていれば、同じような成長パターンをとると仮定できます。この集まりを管理の単位として「林分」と呼び、この林分が集まったものを「森林」とし、森林資源の管理問題を解きやすい形に変えることができます。こうして自然現象を抽象化していき、統計数理モデルとして管理問題を定式化していくと、「間伐や伐採などをいつ、どこで、どれくらい施す必要があるか、林分ごとに解が見えてくる」（吉本教授）とのこと。そして、現場レベルで「ここは今期は切る」「あそこは来期に回す」という明確な計画も最適に立てられるといいます。

野生動物も守ることができる

しかし、昨今、環境保護団体から、野生動物の保護の観点から隣接する林分を同時に伐採するのは回避してほしいという要望などが出るようになりました。また、林業の現場からも、伐採や間伐などの作業をする林分が離れすぎていると作業効率が悪くなるという声も出始めました。そこで林分を集約して伐採する順番を考えるという問題に取り組むことになったのです。「いろいろな方法が考えられてきたが、最近、これは最大フロー問題として捉えられることがわかってきた」と吉本教授。

最大フロー問題とは、ある目的を達成するため、単一の始点から単一の終点に向かって水が流れる最適なフロー経路を見つけるもの。森林資源の管理問題では、林分を抽象化して点として表し、林分の隣接関係に対しては、互いに水を流せる双方向フローとして表現し、さらに終点となる点を森林の中の林分とは別に人工的に外に作り出し、それぞれの点（林分）から終点に向かって水がどの経路を流れるのかを見つけるものです。吉本教授によると、「どこの点（林分）からの水が、どこの経路を通ると、目的（フローの最大化など）を達成できるのかを求めることで、林分をどう集約すればいいかわかってきた」とのこと。さらに手を加えると、集約という空間的なものと、伐採という時間的なものとをリンクできるようになり、集約を考慮できる最適な計画が立てられるようになりました。また、焦点的な集約も可能になり、伐採などの経済活動をしながら保護区を形成することも可能になりました。

これと同じ手法を用いれば、野生動物が森林の中で移動するための経路「コリドー」も守れるといいます。「野生動物や生態系の保護は、現実面では経済活動をしている地域の人たちにとってネガティブな活動ですが、このようにして問題を解けば、野生動物の保護をしながら、かつ地域の人たちの経済活動を維持するという最適な森林資源の管理を探求できます」と、吉本教授はサイエンスベースで取り組む有用さを強調しました。